Answer The Formula for x³ y³ z³ can be derived from the formula of x³ y³ z³ 3xyz x³ y³ z³ 3xyz = (x y z) (x² y² z² – xy – yz– zx) In order to find the formula of x³ y³ z³, we need to send 3xyz to the right side of equal signProve that the equation $x^3y^3z^33xyz=1$ defines a surface of revolution and find the analytical equation of its axis of revolution I think that I need to apply What must be subtracted from 4x^42x^36x^22x6 so that the result is exactly divisible by 2x^2x1?

How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube
X^3+y^3+z^3-3xyz formula
X^3+y^3+z^3-3xyz formula-There are two formula of it 1 x^3 y^3 z^3 3xyz = (xyz) (x^2y^2z^2xyyzzx) 2 x^3 y^3 z^3 3xyz = (1/2) (xyz) {xy)^2(yz)^2(zx)^2}Find the value of x3 y3 z3 3xyz if x y z 12 and x2y2z270 Hint Here, we have to find the value of the algebraic expression We will find the value of the sum of the product of the variables by substituting the given equation in the square of the sum of the three variables' identity



If X Z 225 And Y 226 Then What Is The Value Of X Y Z 3xyz Quora
Answer is (xy z)(x^2 y^2 xyz z^2) You can check by multiplying it out Notice that each term is a perfect cube x^3 y^3 = (xy)^3 So we have a sum of cubes, and the factoring formula is a^3 b^3 = (ab)(a^2abb^2) So we use a = xy and b = z to get x^3 y^3 z^3 = (xy)^3 z^3 = ((xy) z)((xy)^2(xy)zz^2) =(xy z)(x^2 y^2 xyz z^2) check by multiplying itThe algebraic identities for class 9 consist of identities of all the algebraic formulas and expressions You must have learned algebra formulas for class 9, which are mathematical rule expressed in symbols but the algebraic identities represent that the equation is true for all the values of the variables For example; $$\underbrace{x^3y^3}z^33xyz = \underbrace{(xy)^33xy(xy)}z^33xyz$$ $$=\underbrace{(xy)^3z^3}\underbrace{3xy(xy)3xyz} $$ $$=\underbrace{\{(xy)z\}}\{(xy)^2(xy)zz^2\}3xy\underbrace{\{(xy)z\}} \left(\text{ using } a^3b^3=(ab)(a^2abb^2)\text{ for the first two terms }\right) =(xyz)\{(xy)^2(xy)zz^2
Let us consider LHS of the equation LHS = x 3 y 3 z 3 – 3xyz LHS = 1 3 2 3 3 3 – 3(1 × 2 × 3) LHS = 1 8 27 – (3 ×6) LHS = 36 – 18In this question, we will partially differentiate u two times to find the value of k Complete stepbystep answer Now, we will use partial differentiation It is denoted by ∂ We are given u = log ( x 3 y 3 z 3 3xyz) So, partially differentiating u with respect to x, we get ∂ u ∂ x = 3 x 2 3yz ( x 3 y 3 z 3 3xyz)(x^3 y^3 z^3) = (x y z)^3 3{(x)(y)(xy) (y)(z)(yz) (z)(x)(zx)} 6(x)(y)(z) Substituting z for (xy) etc , respectively in the second parenthesis, the RHS reduces to 0 9(x)(y)(z) 6(x)(y)(z) = 3(x)(y)(z)
You can put this solution on YOUR website!Solution x = 2x, y = 2y and z = 4z If x y z = 0, then x 3 y 3 z 3 = 3xyz 8x 3 27y 3 64z 3 = 3 (2x) (2y) (4z) = 48xyz After having gone through the stuff given above, we hope that the students would have understood, "x cube plus y cube plus z cube minus 3xyz" Apart from the stuff given in this section, if you need any other Hint Use the expansion formula of $ {(x y)^3} $ Then replace $ y $ with $ y z $ to write it in three variables Then replace $ y $ with $ y z $ to write it in three variables Further expand it using the condition given in the question and simplify it in the terms of the required result




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



If X Z 225 And Y 226 Then What Is The Value Of X Y Z 3xyz Quora
Answer (1 of 7) First of all, we observe the following formula {{\left( a\,\,b \right)}^{\,3}}\,=\,{{a}^{\,3}}\,\,{{b}^{\,3}}\,\,3\,a\,b\,\left( a\,\,b \right $\begingroup$ By your factorization you could get $\frac{x^{3}y^{3}z^{3} 3xyz}{x y z} xy yz xz = x^{2} y^{2} z^{2}$ Then using a derivative test you can find the minimum $\endgroup$ –X^3y^3z^33xyz= (xyz) (x^2y^2z^2xyyzzx)/a^3b^3c^33abc= (abc) (a^2b^2c^2abbcca) Watch later Share Copy link Info Shopping Tap




Prove That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In




Find The Value Of X3 Y3 Z3 3xyz If X Y Z 12 And X2 Y2 Z2 70 Brainly In
X 3 y 3 z 3 = { (x y z) × (x 2 y 2 z 2 xy yz zx)} 3xyzFormula of polynomials If the polynomial k 2 x 3 − kx 2 3kx k is exactly divisible by (x3) then the positive value of k is ____= 30y 2(x y3)9 (Note Chain rule again, and second term has no y) 3 If z = f(x,y) = xexy, then the partial derivatives are ∂z ∂x = exy xyexy (Note Product rule (and chain rule in the second term) ∂z ∂y = x2exy (Note No product rule, but we did need the chain rule) 4 If w = f(x,y,z) = y xyz, then the partial derivatives are




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Class 9th Ex 2 5 Question 12 Youtube




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube
When you are clear with the logic behind every formula, solving any kind of problem become easier If you are perfect with all the belowmentioned formulas in Maths for Class 9 that is listed chapterwise, nothing can stop you from scoring maximum marks in the final examination ( x^{3} y^{3} z^{3} – 3xyz = (x y z)(x^{2} y^{2(xyz) (x ^ 2 xy y ^ 2 xzyz z ^ 2) หลักฐาน โปรดทราบว่า x = y z เป็นคำตอบของ x ^ 3y ^ 3z ^ 33xyz = 0 เสียบ x = y z ในสมการข้างต้น (y z) ^ 3y ^ 3z ^ 33 (y z) yz = y ^ 3 3y ^ 2z 3yz ^ 2 z ^ 3 y ^ 3z ^ 33y ^ 2z3yz ^ 2 = 0 เราจึงสามารถหารThe formula of x 3 y 3 z 3 – 3xyz is written as \(x^{3} y^{3} z^{3} – 3xyz = (x y z) (x^{2} y^{2} z^{2} – xy – yz – zx)\) Let us prove the equation by putting the values of x = 1;




X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Proof It Lhs To Rhs Brainly In




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In
Calculation ⇒ x 3 y 3 z 3 3xyz = 1/2 × (255 256 257) × (255 256) 2 (256 257) 2 (257 255) 2 Stay updated with the Quantitative Aptitude questions & answers with Testbook Know more about Algebra and ace the concept of Identities(x1) (x2) = x 2 3x 2We know that the formula, x3 y3 z3 −3xyz = (xyz)(x2 y2 z2 −xy−yz−xz) Put the all value in above formula, we get x3 y3 z3 −3xyz = 12×(70−37) = 12×33 =




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube




If X Y Z 0 Then Prove That X3 Y3 Z3 3xyz Youtube
Now, From the second formula x 3 y 3 z 3 3xyz = (x y z)(x 2 y 2 z 2 xy yz zx) ⇒ 12 3xyz = 6(x 2 y 2 z 2 ) (xy yz zx) ⇒ 12 3xyz = 610 13(xyz)^3 (x y z)(x y z)(x y z) We multiply using the FOIL Method x * x = x^2 x * y = xy x * z = xz y * x = xy y * y = y^2Answer The formula of x 3 y 3 z 3 – 3xyz is written as x3y3 z3–3xyz = (xyz)(x2y2z2–xy–yz–zx) x 3 y 3 z 3 – 3 x y z = ( x y z) ( x 2 y 2 z 2 – x y – y z – z x) Let us prove the equation by putting the values of x = 1 y = 2 z = 3 Let us consider LHS of the equation LHS = x 3 y 3 z 3 – 3xyz
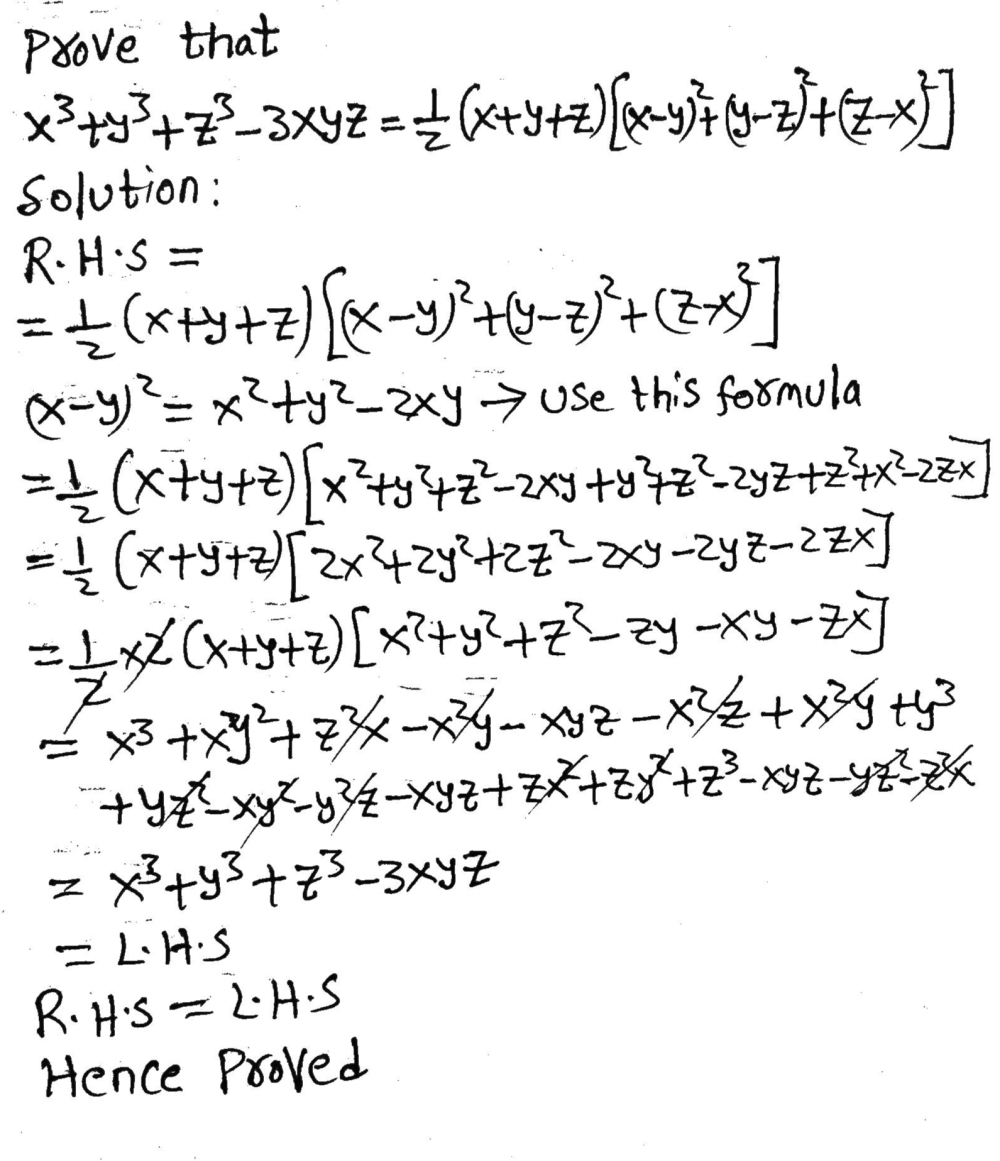



Verify That X 3 Y 3 Z 3 3xyz Frac 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Snapsolve




Find The Value Of X 3 Y 3 Z 3 3xyz If X 2 Y 2 Z 2 And X Y Z 15 Youtube
If x y z = 0, show that x^3 y^3 z^3 = 3xyz (with Video) Ex 25, 13If x y z = 0, show that x3 y3 z3 = 3xyz We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0,x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx)x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence pro First We take RHS & use the Formula ( ab)²= a²b²2ab & simplify it then RHS becomes equal to LHS RHS ⇒ 1/2×(x y z) (x² y²2xy y² z²2yzx²z²2xz) Given x y z = 3, x2 y2 z2 = 45 and x3 y3 z3 = 69 Formula used (x y z)2 = x2 y2 Win over the concepts of Algebra and get a step ahead with the preparations for Quantitative Aptitude with Testbook




印刷可能 X 3 Y 3 X 3 Y 3 Identity




Polynomials Ppt Video Online Download
Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)Learn about Algebra Formula, Equations and List of Basic Algebraic Formulas & Expression in Math Algebra includes real numbers, complex numbers, matrices, vectors and many other topicsBy plugging it into WolframAlpha I've learned that it's $$(xy)(xz)(yz)(xyz)$$ My question is Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers



2



Usylenroiz2jym
Factor x 3 y 3 z 3 − 3 x y z x^3 y^3 z^3 3xyz x 3 y 3 z 3 − 3 x y z The above polynomial is a symmetric polynomial because you can switch any two variables and still get the same polynomial যদি x = 1, y = 2 এবং z = 3 এর মান সন্ধান করে (i) `x^(3) y^(3) z^33xyz` (II) `3xy^(4) 15 x^(2) y 4z` Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous Areas of Parallelograms and Triangles Circles Coordinate Geometry Herons Explanation Calling f (x,y,z) = x3 y3 3xyz − 3 = 0 The gradient of f (x,y,z) at point x,y,z is a vector normal to the surface at this point The gradient is obtained as follows ∇f (x,y,z) = (f x,f y,f z) = 3(x2 yz,y2 xz,xy) at point (1,2, −1) has the value 3( −1,3,2) and the unit vector is { − 1,3,2} √1 32 22 = { −




If X Y Z 0 Then Show That X3 Y3 Z3 3xyz Class 8 Maths Cbse




Mathematics Ii Tranquileducation
Given x = 7, y = 8, and z = 9 Formula used x3 y3 z3 3xyz = (1/2)(x y z)(x y)2 (y z)2 (z x)2 Cal If `xyz=0` show that `x^3y^3z^3=3x y z`Solution (By Examveda Team) Given, x y z = 0 Cubing both side, (x y z) 3 = 0 x 3 y 3 z 3 3xyz = 0 using formula x 3 y 3 z 3 = 3xyz




Ex 2 5 Q No 12 Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




If U Log X 3 Y 3 Z 3 3xyz And X Y Z 2u K X Y Z 2 Then K
x 3 y 3 z 3 3xyz = (xy) 3 3x 2 y 3xy 2 z 3 3xyz = (xy) 3 z 3 3xy (xyz) = (xyz) (xy) 2 z (xy) z 2 3xy (xyz) = (xyz) (x 2 2xyy 2 xzyzz 2 3xy) = (xyz) (x 2 y 2 z 2 xyyzzx) bởi Nguyễn Thanh Huyền Like (1) Báo cáo sai phạm Cách tích điểm HP If `xy=z` prove that `x^(3)y^(3)3xyz=z^(3)` CBSE Class 10 term 1 result 21 in January Know how to Calculate marks, result download process, result date, result time and other details hereThis one is a bit tricky, but anyways Let WLOG x ≤ y ≤ z and let y = a x, z = b x Now plug this into Now this is linear in x Hence we may take x = 0 to achieve the minimum of LHS This gives We take a = t b with t ≥ 1 Then C max = min t ≥ 1 t 3 1 t ( t − 1) Which I



1




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5
prove that (xy)3(yz)3(zx)33(xy) (yz) (zx) =2(x3y3 z 3 3xyz) Maths Polynomials




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Show That X3 Y3 Z3 3xyz X Y Z X2 Y2 Chegg Com




Pdf On Solving The Diophantine Equation 𝑥 𝑦 𝑧 𝑘 On A Vector Computer




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube




New Question Verify That X3 Y3 Z3 3xyx 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Tex Textless H2 Brainly In




48 Mathematics Example 24
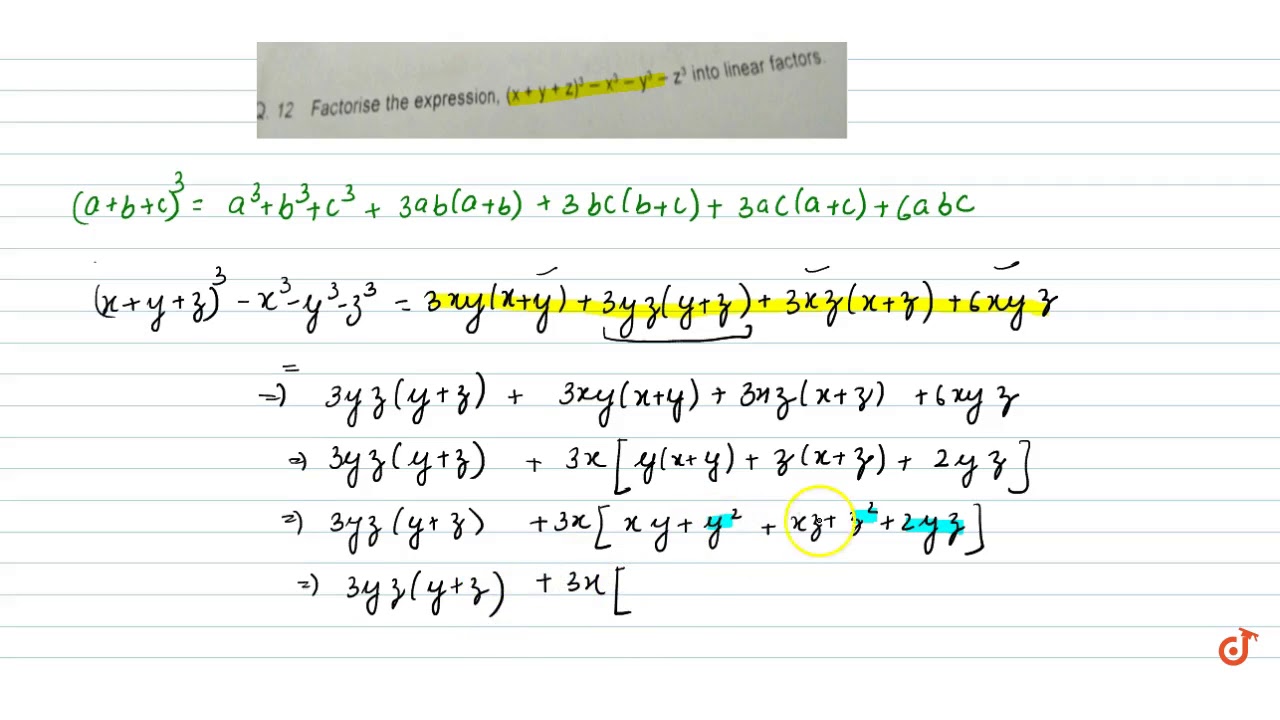



Q 12 Factorise The Expression X Y Z 3 X3 Y3 Z3 Into Linear Factors Youtube




2 Polynomials Note Blast




Verify That X3 Y3 Z3 3xyz X Y Z 2 X Y Y Z X Z Brainly In




If X Y Z 9 And Xy Yz Zx 23 The Value Of X 3 Y 3 Z 3 3xyz
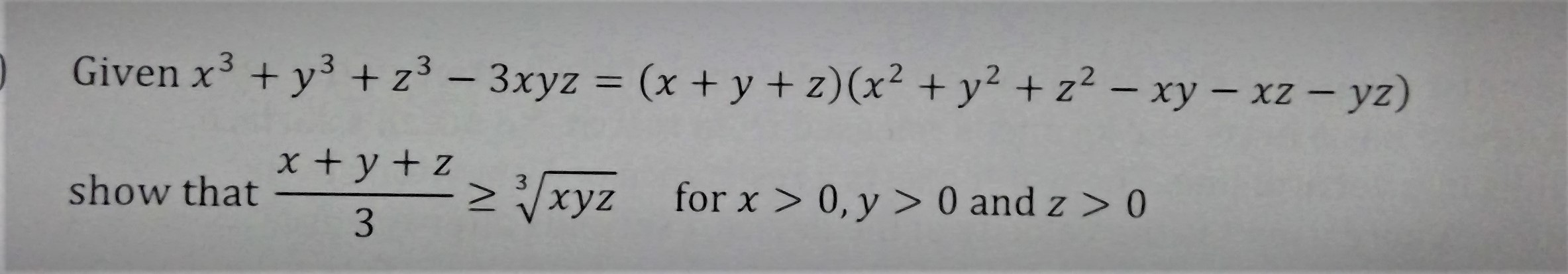



Solved 0 Given X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Chegg Com




X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55




If X Y Z 0 Show That X 3 Y 3 Z 3 3x Y Z
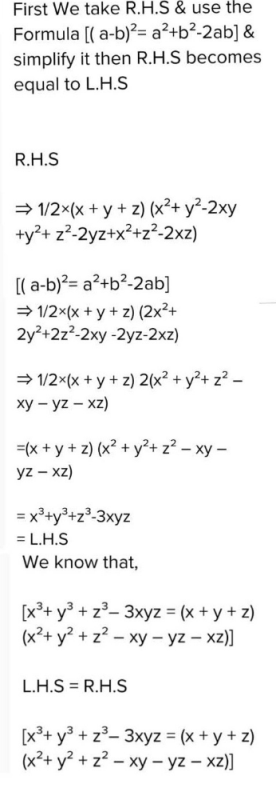



Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Can Any One Solve This Question Edurev Class 9 Question
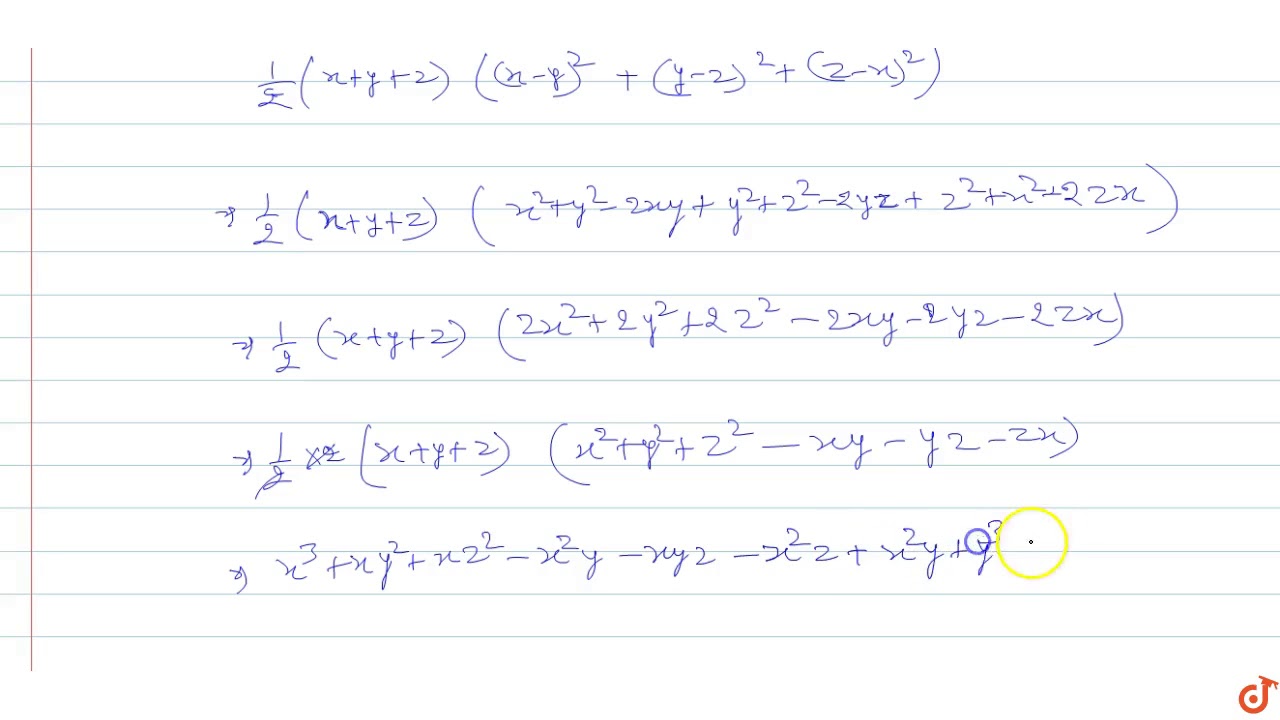



Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube



X3 Y3 Z3 3xyz




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




Top 18 X 3 Y 3 Z 3 Formula Mới Nhất




Pdf On Solving The Diophantine Equation 𝑥 𝑦 𝑧 𝑘 On A Vector Computer




Evaluate X3 Y3 Z3 3xyz When X 2 Y 1 And Z 3 Brainly In




File
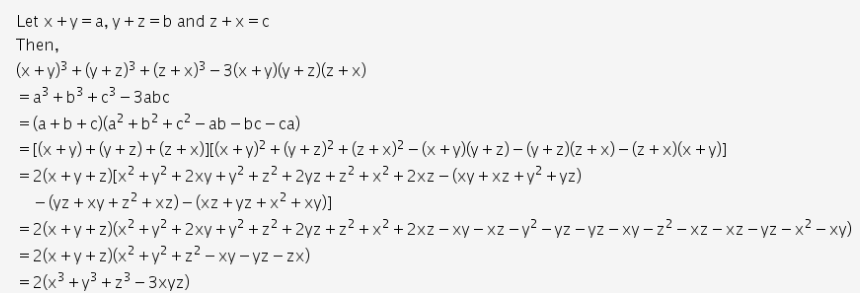



X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Cbse Class 9 Maths Learn Cbse Forum




Exercise




Prove That X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Brainly In



How To Divide X 3 Y 3 Z 3 3xyz By X Y Z Quora




If X3 Y3 Z3 3 1 Xyz P Y Z X Q Z X Y And R X Y Z Then What Is The Value Of P3 Q3 R3 3pqr Quora




Ex 2 5 11 Factorise 27 X3 Y3 Z3 9xyz Class 9 Ex 2 5




2 Two Cube 5 Five Cube 10 Ten Cube Pdf Free Download



X Y Z 2




If X Y Z 0 Then Find The Value Of X3 Y3 Z3 Brainly In




Pdf On Solving The Diophantine Equation 𝑥 𝑦 𝑧 𝑘 On A Vector Computer




Factoring Formulas In Algebra What Are Factoring Formulas



If 1 X 1 Y 1 Z 0 And X Y Z 9 Then What Is The Value Of X 3 Y 3 Z 3 3xyz Quora




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




Log9x Log 3 X 3 2 Detailed Login Instructions Loginnote




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In




If X Y Z 0 Then Prove That X3 Y3 Z3 3xyz By X Y 3 Brainly In




Factorization Of X3 Y3 Z3 3xyz Youtube



What Is The Formula Of Math X 3 Y 3 Z 3 3xyz Math Quora




Using Identity Viii X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Solve The Following Question 8x3 Y3 27z3 18xyz Maths Polynomials Meritnation Com
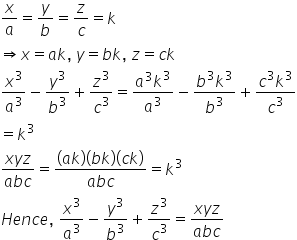



If X A Y B Z C Then Show That X3 A3 Y3 Z3 A Xyz Abc Mathematics Topperlearning Com Mfmw0q55




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz Brainly In




Prove That X3 Y3 Z3 3xyz Half X Y Z X2 Y2 Y2 Z2 Z2 X2 Rn Maths Polynomials Meritnation Com



1




If X Y Z 0 Then Show That X3 Y3 Z3 3xyz



If X Z 225 And Y 226 Then What Is The Value Of X Y Z 3xyz Quora




If X Y Z 0 Show That X3 Y3 Z3 3xyz Maths Polynomials Meritnation Com




Answers




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Important Question For Exams Of Ix Youtube
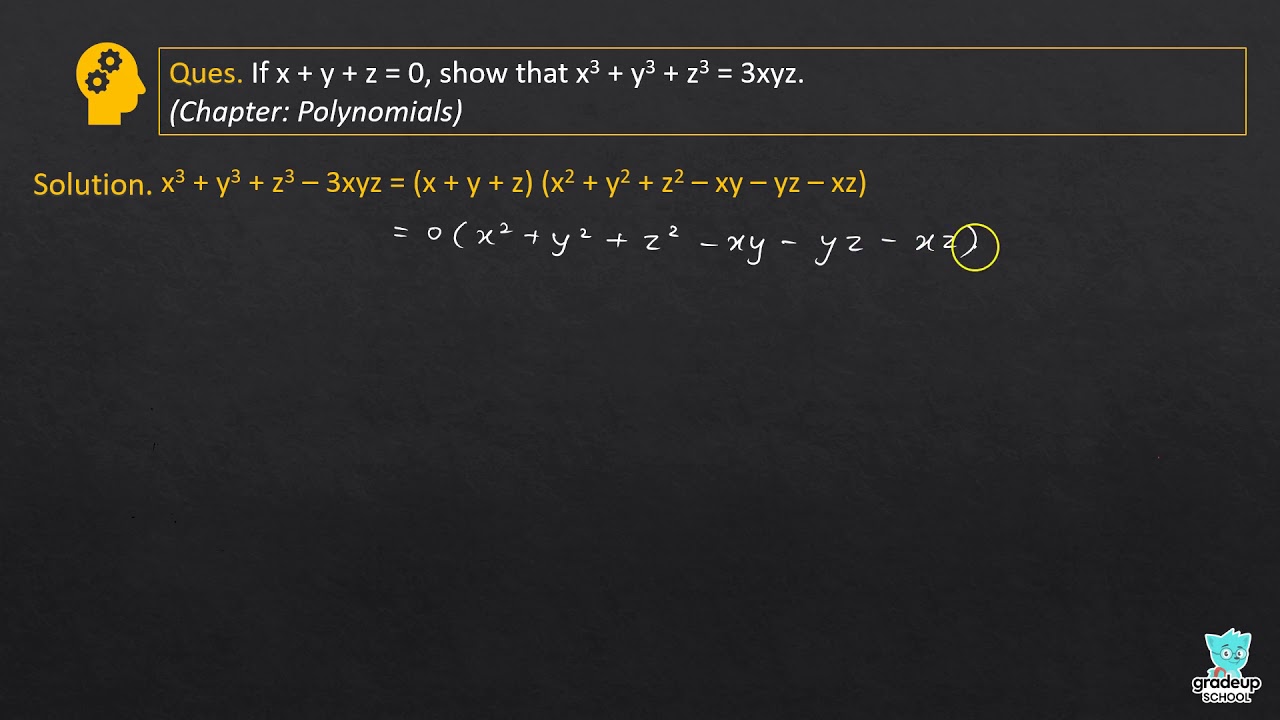



Ex 3 5 Q11 If X Y Z 0 Then Verify That X 3 Y 3 Z 3 3xyz



Math Grinnell Edu




Bits Of Math Problem Cubes And Cube Roots
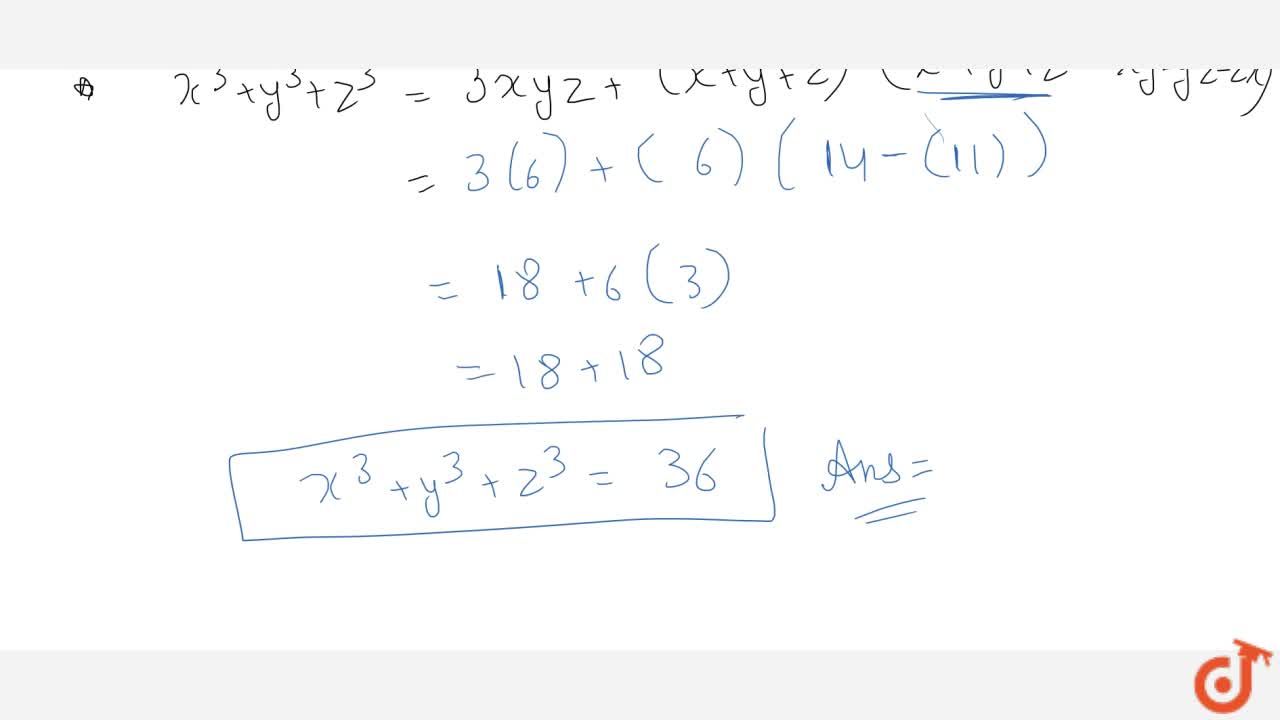



If X Y Z 6 And Xy Yz Zx 11 And Xyz 6 Is Given Find The Value Of X 3 Y 3 Z 3




Evaluate X 3 Y 3 Z 3 3xyz When X 2 Y 1 And Z 3




Mathematics Complex Numbers Session Session Objectives Ppt Download




印刷可能 X 3 Y 3 X 3 Y 3 Identity




If X Y Z 0 Then Show That X Cube Y Cube Z Cube 3xyz Mathematics Topperlearning Com Vj2f0044




If X Y Z 0 Show That X3 Y3 Z3 3xyz Scholr




Polynomials Ppt Video Online Download




X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Proof It Lhs To Rhs




Solving A Quadratic Equation By Factoring A Plus Topper




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In




Prove That X Y3 Y Z3 Z X3 3x Yy Zz X 2x3 Y3 Z3 3xyz Maths Polynomials Meritnation Com




Prove That X3 Y3 Z3 3xy X Y Z X2 Y2 Z2 Xy Yz Zx Only By Lhs Brainly In



How To Prove That If X Y Z 0 Then X Y Z 3xyz Quora



Cbse 9 Math Cbse Polynomials Ncert Solutions
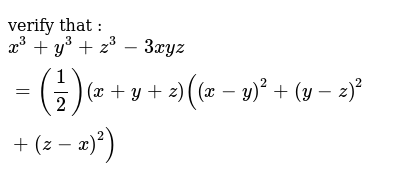



Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2
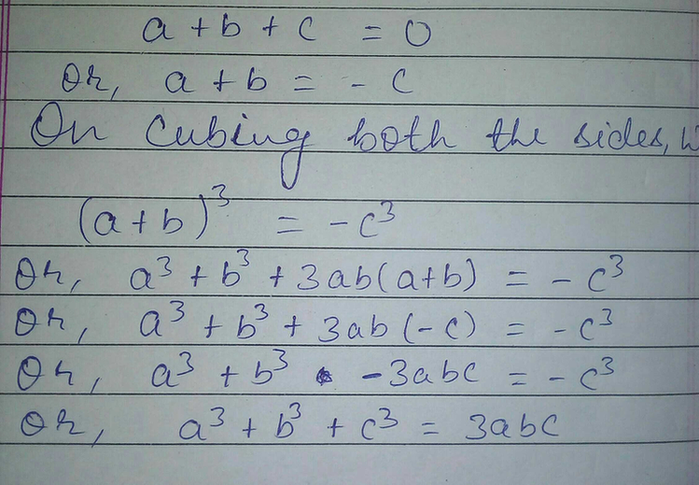



If X Y Z 0 Show That X3 Y3 Z3 3xyz Scholr




The Equation 3y Z 3 3xz Defines Z Implicitly As A Function Of X And Y Evaluate All Three Second Partial Derivatives Of Z With Respect To X And Or Y Verify That Z Is A




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video




2




Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z Z X 2




If X 1 3 Y 1 3 Z 1 3 0 Then What Is X Y Z 3 Equal To




New Solutions Of 1 Download Table




Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2




If X Y Z 0 Show That X3 Y3 Z3 3 Xyz Brainly In



2




If Math X Y Z 0 Math What Is The Value Of Math Frac X 2 Yz Frac Y 2 Zx Frac Z 2 Xy Math Quora



If Math X Y Z 0 Math How Do You Prove That Math X 3 Y 3 Z 3 3xyz Math Quora



If X Y Z 6 And Xy Yz Zx 10 Then What Is The Solution Of X 3 Y 3 3xyz Quora




I Need An Example For This Formula X3 Y3 Z3 3xyz Brainly In




If X Y Z 0 Then Show That X3 Y3 Z3 3xyz If X Y Z 0 Prove That X3 Y3 Z3 3xyz Youtube



0 件のコメント:
コメントを投稿