[最も選択された] expand (1/x y/3)^3 232524

 The expansion is y^55y^4x10y^3x^210y^4x^35y^5x^4x^5 We need to use Pascal's Triangle, shown in the picture below, for this expansion Because the binomial is raised to the 5th power, we need to use the 5th row of the triangleCreated by T Madas Created by T Madas Question 3 (**) y x= e sin32x a) Use standard results to find the series expansion of y, up and including the term in x4 b) Hence find an approximate value for 01 2 0 e sin3x x dx FP2M , e sin3 3 6 52 2 3 4 53 ( ) 2 x x x x x x O x= − ,Expandcalculator expand \left(x1\right)^{3} en Related Symbolab blog posts Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series Over the next few weeks, we'll be

Binomial Expansion Made Easy Expand X Y Algebra Youtube

Expand (1/x y/3)^3

Expand (1/x y/3)^3-Start your free trial In partnership with You are being redirected to Course Hero I want to submit the same problem to Course Hero CancelExpand each logarithm 1) ln (x6y3) 2) log 8 (x ⋅ y ⋅ z3) 3) log 9 (33 7) 4 4) log 7 (x3 y) 3 5) log 8 (a6b5) 6) log 4 (63 ⋅ 113) 7) log 3 (u3 v) 2 8) ln 3 u ⋅ v ⋅ w 9) log 6 (3 ⋅ 2 ⋅ 56) 10) log 4 (2 ⋅ 11 ⋅ 74) 11) log 6 (c5 3 a) 12) ln (5 2 2) 5 13) log 5 (x3 y) 6 14) log 4 (73 3

How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube

 How do you use the binomial theorem to expand #(x^(2/3)y^(1/3))^3#?An outline of Isaac Newton's original discovery of the generalized binomial theorem Many thanks to Rob Thomasson, Skip Franklin, and Jay Gittings for theirCalculus questions and answers 1 Use the laws of logarithms and expand 100 (x24) a) log G ) (x2 1) (x7)2 ,9x2 (y3), b) log36 3x22 2 Use the laws of logarithms and combine a) logab clogad rlogas b) 2 (log3x log3y 310g32) 3 Solve the equation log (2x) log (x 1) 2 = 8 = log (3x) 4 Find the interest rate needed for an investment

⋅(x)6−k ⋅(−1)k ∑ k = 0 6 ⁡(x y) 7 = x 7 7x 6 y 21x 5 y 2 35x 4 y 3 35x 3 y 4 21x 2 y 5 7xy 6 y 7 When the terms of the binomial have coefficient(s), be sure to apply the exponents to these coefficients Example Write out the expansion of (2x 3y) 4 Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 31 Question 1 Complete the table Question 2 Find the product of the terms Question 3 If l = 4pq 2, b = 3p 2 q h = 2p 3 q 3 then, find the value of l × b × h Question 4 Question 5

Answer (1 of 4) I got the answer Following is to be learned Source GATE4800 1 1 621 Practice Set 52 1 Expand 1 k 4 3 2 7 x 8 y 3 3 7 m 3 4 from CIS NETWORKS at Abbey CollegeRead It /1 Points DETAILS WANEFMAC7 113 Compute the indicated derivative od 1(x2 x)(x2 – x

What Is The Answer Of X Y Quora

2

👉 Learn all about sequences In this playlist, we will explore how to write the rule for a sequence, determine the nth term, determine the first 5 terms orExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionalsAnswer (1 of 5) First of all, we observe the following formula {{\left( a\,\,b \right)}^{\,3}}\,=\,{{a}^{\,3}}\,\,{{b}^{\,3}}\,\,3\,a\,b\,\left( a\,\,b \right

Expand Tan 1y X About The Point 1 1 Using Taylor S Theorem Up To The Second Degree Terms Sarthaks Econnect Largest Online Education Community

Please Expand 1 X Y 3 Whole Cube Brainly In

Section 35 Minterms, Maxterms, & Canonical Forms Page 2 of 4 A maxterm, denoted as Mi, where 0 ≤ i < 2n, is a sum (OR) of the n variables (literals) in which each variable is complemented ifML Aggarwal Solutions for Class 9 Maths Chapter 3 – Expansions are provided here to help students prepare and excel in their exams This chapter mainly deals with problems based on expansions Experts tutors have formulated the solutions in a step by step manner for students to grasp the concepts easily From the exam point of view, solvingBinomial Expansions Binomial Expansions Notice that (x y) 0 = 1 (x y) 2 = x 2 2xy y 2 (x y) 3 = x 3 3x 3 y 3xy 2 y 3 (x y) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4 Notice that the powers are descending in x and ascending in yAlthough FOILing is one way to solve these problems, there is a much easier way

4 The Binomial Theorem

Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange

4 Binomial Expansions 41 Pascal's riTangle The expansion of (ax)2 is (ax)2 = a2 2axx2 Hence, (ax)3 = (ax)(ax)2 = (ax)(a2 2axx2) = a3 (12)a 2x(21)ax x 3= a3 3a2x3ax2 x urther,F (ax)4 = (ax)(ax)4 = (ax)(a3 3a2x3ax2 x3) = a4 (13)a3x(33)a2x2 (31)ax3 x4 = a4 4a3x6a2x2 4ax3 x4 In general we see that the coe cients of (a x)nFind the product of two binomials Use the distributive property to multiply any two polynomials In the previous section you learned that the product A (2x y) expands to A (2x) A (y) Now consider the product (3x z) (2x y) Since (3x z) is in parentheses, we can treat it as a single factor and expand (3x z) (2x y) in the same(xy) 5 = x 5 5x 4 y 10x 3 y 2 10x 2 y 3 5xy 4 y 5 There are several things that you hopefully have noticed after looking at the expansion There are n1 terms in the expansion of (xy

How To Expand The Binomial X Y 10 Quora

Using The Binomial Theorem College Algebra

Then x^2y^2=y^22nyn^2y^2=2nyn^2=n(2yn) Thus, n and 2yn must be complementary factors of 33 1 and 33, or 3 and 11Maclaurin Series of ln (1x) In this tutorial we shall derive the series expansion of the trigonometric function ln ⁡ ( 1 x) by using Maclaurin's series expansion function Consider the function of the form f ( x) = ln ⁡ ( 1 x) Using x = 0, the given equation function becomesRead It /1 Points DETAILS WANEFMACZ Calculate dy dx You need not expand your answer x² 66 1 y = x2 x 3x 1 dy dx Need Help?

What Is The Binomial Expansion For 1 X 1 Quora

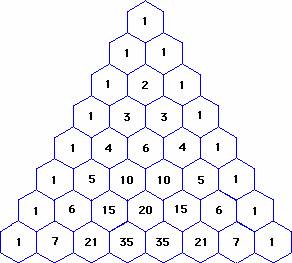
How Do You Expand X 3 5 Using Pascal S Triangle Socratic

Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!⋅(1)3−k ⋅(−x)k ∑ k = 0 3 ⁡Expand (xy)^3 (x y)3 ( x y) 3 Use the Binomial Theorem x3 3x2y3xy2 y3 x 3 3 x 2 y 3 x y 2 y 3

Binomial Expansion And Series A Level Maths Uptuition With Mr Will

Binomial Expansion Made Easy Expand X Y Algebra Youtube

Multiply both sides of the equation by 3 x y, the least common multiple of x y, 3 Use the distributive property to multiply 3 by 2x^ {2}5y^ {2} Use the distributive property to multiply 3 by 2 x 2 − 5 y 2 Subtract xy from both sides Subtract x y from both sidesExpand using the Binomial Theorem (x3)^3 Use the binomial expansion theorem to find each term The binomial theorem states Expand the summation Simplify the exponents for each term of the expansion Simplify each term Tap for more steps Multiply by Anything raised to isThe Binomial Theorem is the method of expanding an expression which has been raised to any finite power A binomial Theorem is a powerful tool of expansion, which has application in Algebra, probability, etc Binomial Expression A binomial expression is an algebraic expression which contains two dissimilar terms Ex a b, a 3 b 3, etc

X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube

How Do You Use The Binomial Theorem To Expand X Y 5 Socratic

The calculator allows you to expand and collapse an expression online , to achieve this, the calculator combines the functions collapse and expand For example it is possible to expand and reduce the expression following ( 3 x 1) ( 2 x 4), The calculator will returns the expression in two forms expanded and reduced expression 4 14 ⋅ xExpand 1/12*((xyz)^6 2(x^6y^6z^6) 2(x^3y^3z^3)^2 4(x^2y^2z^2)^3 3(xyz)^2(x^2y^2z^2)^2) Natural Language;Answer (1 of 11) (1x)^1=1xx^2x^3__&__ up to infinity

Taylor Series Wikipedia

1 Expand Y 3 X 2 Brainly In

 Explanation (x −y)3 = (x − y)(x −y)(x −y) Expand the first two brackets (x −y)(x − y) = x2 −xy −xy y2 ⇒ x2 y2 − 2xy Multiply the result by the last two brackets (x2 y2 −2xy)(x − y) = x3 − x2y xy2 − y3 −2x2y 2xy2 ⇒ x3 −y3 − 3x2y 3xy2 Always expand each term in the bracket by all the otherPiece of cake Unlock StepbyStep expand (x1) (x2) (x3) Natural Language Math Input NEW Use textbook math notation to enter your math Try it × Extended KeyboardExpand (xy1) (xy1) (xy1) (xy1) 1 Simplify x y × 1 xy\times 1 xy ×1 to x y xy xy

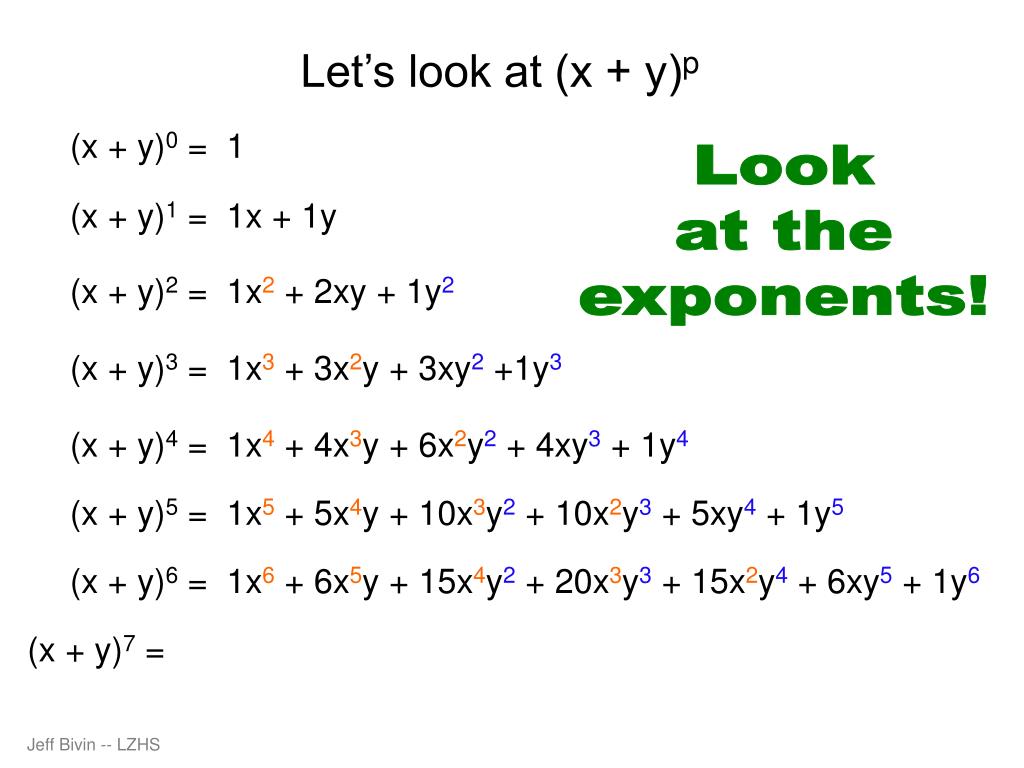
Ppt Binomial Expansion And More Powerpoint Presentation Free Download Id

Unit 11 Logarithms Day 3 3 Properties To

Expand 1 2 x 3 We pick the coefficients in the expansion from the row of Pascal's triangle (1,3,3,1) Powers of 2 x increase as we move left to right Any power of 1 is still 1 1 2 x 3 = 1(1)3 3(1)2 2 x 3(1)1 2 x 2 1 2 x 3 = 1 6 x 12 x2 8 x3 Exercises 2Since, x 3 3 x 2 y 3 x y 2 y 3 = (x y) 3 Let's factorize another polynomial This has both positive and negative terms, so it can be compared with the expansion of ( x − y ) 3Algebra Expand using the Binomial Theorem (x1)^6 (x − 1)6 ( x 1) 6 Use the binomial expansion theorem to find each term The binomial theorem states (ab)n = n ∑ k=0nCk⋅(an−kbk) ( a b) n = ∑ k = 0 n ⁡ n C k ⋅ ( a n k b k) 6 ∑ k=0 6!

Expanding Binomials Video Series Khan Academy

Expand 1 3 X 2 3 Y Whole Cube Brainly In

Algebra Expand using the Binomial Theorem (1x)^3 (1 − x)3 ( 1 x) 3 Use the binomial expansion theorem to find each term The binomial theorem states (ab)n = n ∑ k=0nCk⋅(an−kbk) ( a b) n = ∑ k = 0 n ⁡ n C k ⋅ ( a n k b k) 3 ∑ k=0 3!The masses in grams of X, Y and Z present at time t seconds after the start of the reaction are x, 10 – x and – x respectively At any time the rate of formation of X is proportional to the product of the masses of Y and Z present at the time When t = 0, x = 0 and d d t x = 2 (a)Show that x and t satisfy the differential equation d d tExpand\3(x6) expand\2x(xa) expand\(2x4)(x5) expand\(2x5)(3x6) expand\(4x^23)(3x1) expand\(x^23y)^3;

Learn Algebraic Identity Of X Y And X Y In 3 Minutes

Taylor Series Expand X 2y 3y 2 In The Powers Of X 1 And Y 2 Up To 3 Degree Terms Youtube

 expand option it deals with the expansion of parent widget The problem is that these two sound more or less the same I even tried out a few examples by toggling between the 4 values of fill and 2 values of expand but received more or less the same output in 2 or 3 cases, because of which I have this query Any help would be appreciated inExpand (3 x 2) 3 Mathematics Concise Mathematics Standard VIII Q3 Factorise 6 x 2 y 9 x y 2 4 y 3 Mathematics Q4 Simplify (3 x 4 y) 3The binomial expansion of a difference is as easy, just alternate the signs (x y) 3 = x 3 3x 2 y 3xy 2 y 3In general the expansion of the binomial (x y) n is given by the Binomial TheoremTheorem 671 The Binomial Theorem top Can you see just how this formula alternates the signs for the expansion of a difference?

Is There A Shortcut To Expand The Equation X Y Quora

Solved Name Group Math 115 Spring Problem 3 Chegg Com

Harnett, ch 3) A The expected value of a random variable is the arithmetic mean of that variable,Expectations Expectations (See also Hays, Appendix B;Expand (x1)^2 Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each term Tap for more steps Multiply by Move to the left of

Year 12 C1 Binomial Theorem Task Expand The Following 1 X Y 1 2 X Y 2 3 X Y 3 4 X Y 4 What Do You Notice Powers Of X Start From Ppt Download

Taylor Series Wikipedia

  Step 1 The given logarithm expression can be expanded using following properties of logarithms The exponent property is log a x y = y log a x The sum property of logarithms is log a x log a y = log a x y The difference property of logarithms is log a x − log a y = log a x y Step 2 The given expression is log 3 3 x 5 yPrecalculus The Binomial Theorem The Binomial Theorem 1 AnswerBinomial Theorem Examples Example 1 Expand the given equation (x/2 3/y)4 Sol Using the equation, ( x y) n = ∑ i = 0 n n C r x n − r y r , we get x 2 3 y) 4 = 4 C 0 ( x 2) 4 4 C 1 ( x 2) 3 ( 3 y) 4 C 2 ( x 2) 2 ( 3 y) 2 4 C 3 ( x 2) ( 3 y) 3 4 C 4 ( 3 y) 4

Please Expand 1 X Y 3 Whole Cube Brainly In

2

Read It Watch It Calculate dy dx You need not expand your answer X7 7 y = VX 7 dy dx II Need Help?

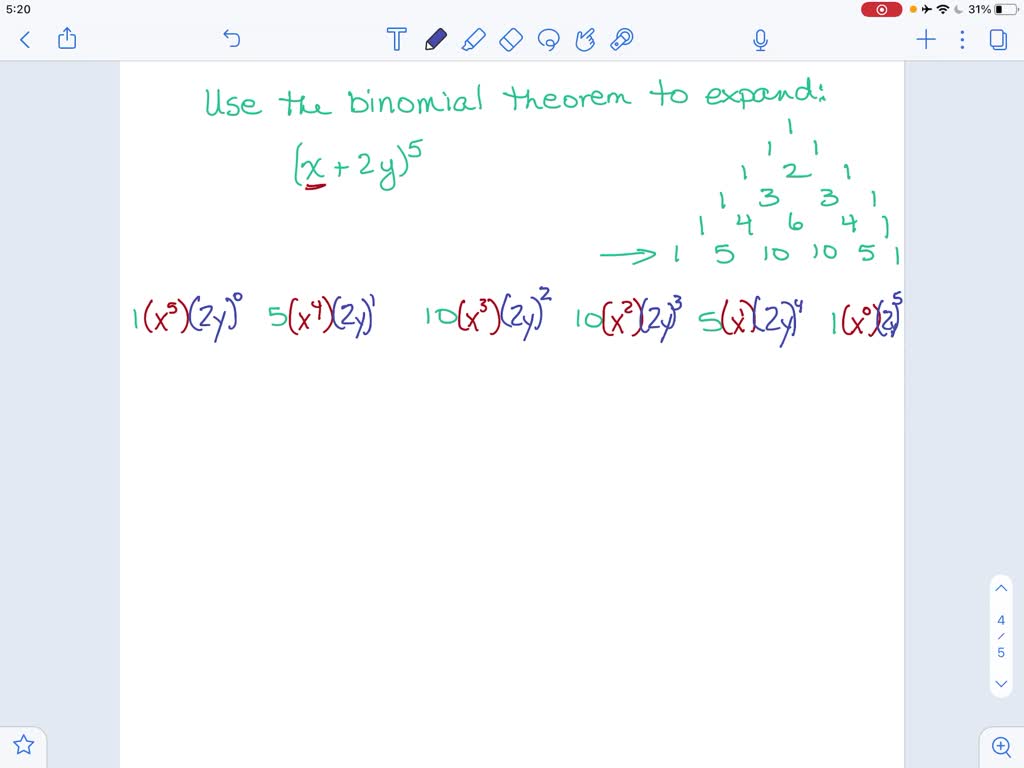
Solved Find The General Solution Of R T X Y Bv Using Binomial Theorem To Expand It

Question Partial Fraction From Pure Math Of A Level Paper

How Can We Expand X Y 1 2 Youtube

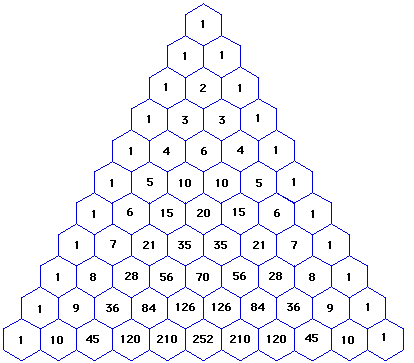
How Do You Expand X Y 10 Socratic

How To Expand 1 1 2x 1 3x In A Series Of Ascending Powers Of X And Find When The Expansion Is Valid Quora

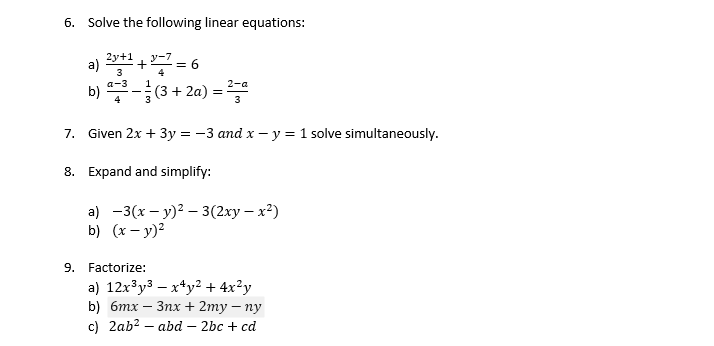
Solved 6 Solve The Following Linear Equations A 2y 1 3 Chegg Com

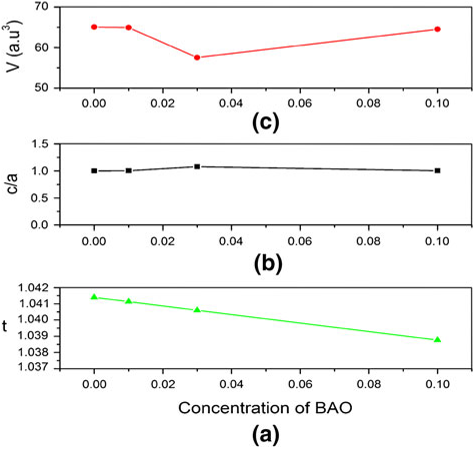
Investigation Of Structural And Diffuse Phase Transition Of New Nano Lead Free System Xbao Ybzt 1 X Y t Iit Madras

Wkrk3kmybxxf3m

How Do You Use Pascals Triangle To Expand 2y X 5 Socratic

Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange

Section 8 5 The Binomial Theorem Ppt Download

9 Binomial Theorem Example 4 Expanding 3 Terms In A Binomial Question Youtube

9 5 The Binomial Theorem

Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9

1 Expand X Y 5 Using Binomial Theorem Youtube

Is There A Shortcut To Expand The Equation X Y Quora

X 2 2y 3 1 X Y 3 3 Solve The Given Equation Using Elimination And Substitution Method Youtube

Expand 1 X Y 3 3 Solve It Fastly Brainly In

Expand And Simplify Binomial Squares 2x 3y 2 Youtube

Expand 1 X Y 3 3 Using Identity Brainly In

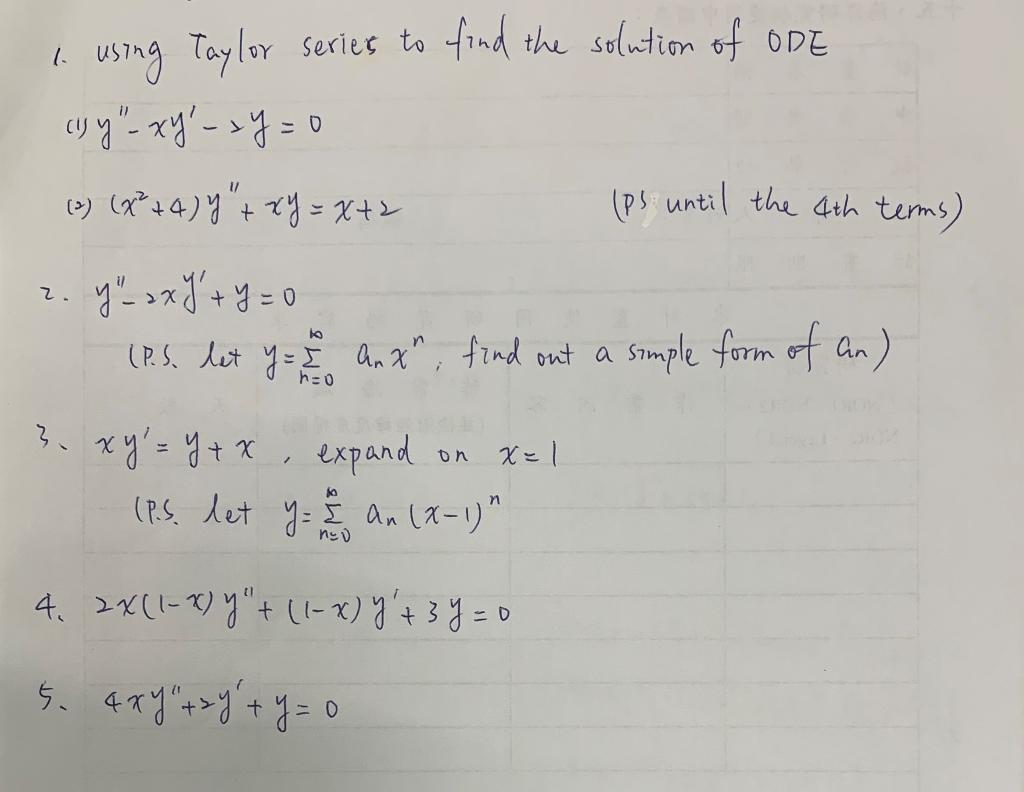
Solved 1 Using Taylor Series To Find The Solution Of Ode Chegg Com

Architectures Of Dna A B C D Mb X Y Y Stands For An Inverted Download Scientific Diagram

How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube

Solved Use The Binomial Series To Expand The Function As A Chegg Com

Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf

Using Binomial Theorem Expand X Y 5 X Y 5 Dot And Hence Find The Value Of Sqrt 2 1 Youtube

Pdf Developing Proof Comprehension And Proof By Contradiction Through Logical Outlines Semantic Scholar

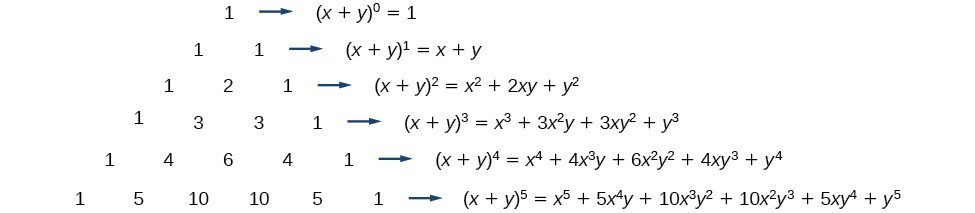
Using The Binomial Theorem College Algebra

Simplify The Expression Ppt Video Online Download

If The First Three Terms In The Expansion Of 1 Ax N In The Ascending Power Of X Are 1 12x 64x 2 What Will Be A And N Quora

Example 6 Show That Middle Term In Expansion Of 1 X 2n Is

Binomial Expansion Formulas Derivation Examples

Using Binomial Theorem Expand X Y 5 X Y And Hence Find The Value Of Root 2 1 5 Root 2 1 5 Maths Binomial Theorem Meritnation Com

10 Factorise 1 A B2ab 11 Expand 3b 1 2 3 Verify Each Of The F

A B Whole Cube

Simplifying Expressions

Write Down The Expansion By The Binomial Theorem Of 3 X Y 2 To The Power Of Maths Binomial Theorem Meritnation Com

Find The Coefficient Of X 6y 3in The Expansion Of X 2y 9

9 5 The Binomial Theorem Let S Look At The Expansion Of X Y N Ppt Video Online Download

How Do You Expand X Y 6 Using Pascal S Triangle Socratic

X Y 2 Expand Aoierrico

Taylor Series Wikipedia

Mathematics Support Centre Title Brackets

1 X Y 3 3 Expand Brainly In

Your Math Tutor For All Incoming Grade 11 Stem Students Pre Calculus Topic Conic Sections With Detailed Solutions Para Mas Lalong Maitindihan Sharing Is Caring A Thread T Co Tbw6mdwt2o Twitter

Ppt The Binomial Theorem Powerpoint Presentation Free Download Id

Binomial Expansion Binomial Expansions Copyright C By Houghton Mifflin Company Inc All Rights Reserved 2 The Binomial Theorem Provides A Useful Method Ppt Download

Find The Expansion Of X Y 1 Whole Cube Brainly In

How Do You Find The Coefficient Of X 6 In The Expansion Of 2x 3 10 Socratic

1

J23

Expand 1x Y3 3 Maths Questions

X Y 4 Expand

Plos One Investigating Cd99 Expression In Leukemia Propagating Cells In Childhood T Cell Acute Lymphoblastic Leukemia

9 5 The Binomial Theorem Lets Look At

Solved Vii Bernoulli Equations 2 Of 8 1 V Y Ey 2 V Y Chegg Com

How Do You Find The Binomial Expansion Of X Y 7 Socratic

Solved Question 1 A Rearrange The Following Expressions To Chegg Com

How Do You Use The Binomial Series To Expand X Y 6 Socratic

Pdf Collection Description And Visualization Of The German Reddit Corpus Semantic Scholar

J23

Expand Tan 1y X About The Point 1 1 Using Taylor S Theorem Up To The Second Degree Terms Sarthaks Econnect Largest Online Education Community

The Factors Of X 3 1 Y 3 3x Y Are A X 1 Y X 2 1 Y 2 X Y X Y B X Y 1 X 2 Y 2 1 X Y X Y C X 1 Y X 2 1 Y 2 X Y X Y D 3 X Y 1 X 2 Y 2 1

T Expand The Following A B 1 3 B C 3 3 C 2x 3 3 D X 2 Y 2 C 5 3y 3 F Xy 2a 3 Snapsolve

Expand X Y 3 And X Y 2 Brainly In

Mathwithmsanthony Weebly Com

A Quick And Efficient Way To Expand Binomials Ppt Download

Expand 1 X Y 3 Whole Cube Studyrankersonline

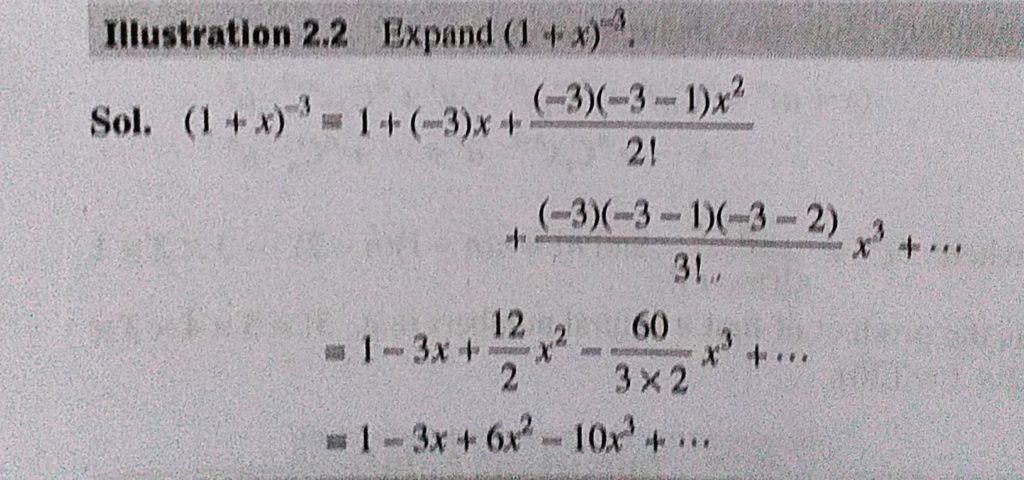
Expand 1 X 3 Sahay Lms

Expand X 2 2y 5 Using Binomial Expansion Youtube

My First Expansion Hope You Guys Enjoy Expanddong

8 5 The Binomial Theorem Warm Up Copyright C By Houghton Mifflin Company Inc All Rights Reserved 2 X Y 3 X 3 3x 2 Y 3xy 2 Y Ppt Download

3 An Emaxima Session Download Scientific Diagram

Solved 2 Use The Binomial Expansion To Expand Y X Chegg Com

Pokemon Tcg Xy Steam Siege 3 Booster Packs Coin Rayquaza Promo Card Pokemon Center Canada Official Site